miércoles, 28 de mayo de 2014

FORMULAS PARA OBTENER LOS ANGULOS INTERNOS DEL PENTÀGONO :3

Propiedades


A = \frac{5a^2}{4}\cot \frac{\pi}{5} = \frac {a^2}{4} \sqrt{25+10\sqrt{5}} \simeq 1,72048 a^2
De forma general si tenemos que el radio de la circunferencia circunscrita es ru
A=\frac{5}{8}\cdot r_u^2 \cdot \sqrt{10+2\sqrt{5}}
o también:
A=\frac{5}{2}\cdot r_u^2 \cdot \sin{72^\circ}

Perímetro

Siempre que supongamos que el pentágono tiene lado a:
a=2 \cdot r_u \cdot \cos 54^\circ
ó también:
a=r_u \cdot \sqrt{\frac{5 - \sqrt{5}}{2}}
Para obtener el perímetro P de un pentágono regular, multiplíquese la longitud t de uno de sus lados por cinco (el número de lados n del polígono).
P = n\cdot t = 5\ t

Fórmula para calcular los ángulos interiores

La suma de todos los ángulos interiores de un pentágono es de 540°.
La fórmula general para calcular la suma de los ángulos interiores de cualquier polígono regular (en el caso del pentágono n = 5) es:
\sum {\alpha =}(n - 2) \cdot 180^\circ = 3 \cdot 180^\circ = 540^\circ
El ángulo comprendido entre dos lados de un pentágono regular se puede calcular mediante la siguiente fórmula (en el pentágono, n = 5):
\alpha =\frac{(n - 2)}{n} \cdot 180^\circ = \frac{3}{5} \cdot 180^\circ = 108^\circ

Construcción de un pentágono regular

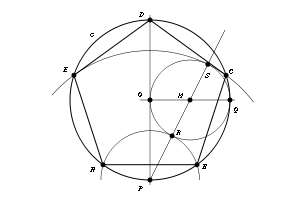
Pentagon construction.svg
Podemos construir con regla y compás un pentágono regular, inscrito en una circunferencia (véase la figura) de la siguiente manera:
Trazamos dos rectas perpendiculares por el centro O de la circunferencia (PD y OQ en la figura). Determinamos el punto medio M del segmento OQ y trazamos la recta PM. Con centro en M, trazamos la circunferencia de radio MO. Denotemos con R y S las intersecciones de esta circunferencia con la recta PM. Las circunferencias de centro en P y radios PR y PS determinan los vértices del pentágono regular.
Uniendo los vértices del pentágono, se obtiene un pentagrama (estrella de 5 puntas) inscrito en él. En el centro quedará otro pentágono regular, con lo que el proceso de inscribir pentagramas en los sucesivos pentágonos que se vayan generando, matemáticamente, no tiene fin.
Al inscribir en un pentágono regular un pentagrama, se puede observar la razón áurea entre las longitudes de los segmentos resultantes.

Relaciones geométricas del pentágono regular

Relación con el número áureo


Pentagrama y pentágono
Veamos que la razón entre un segmento que una dos de sus vértices no consecutivos y uno de los lados del pentágono es la razón aúrea o número áureo, por ejemplo que
CE = \left(\frac{1 + \sqrt5}2\right)CD
Por simetría, los segmentos CE y CA son iguales. Observamos que los triángulos ANF y CMF son semejantes. De la semejanza de sus lados tenemos que
\frac{MC}{AN} = \frac{FC}{AF}
Observemos que MC es la mitad de CE y que AN es la mitad de AB. Por otra parte, como el triángulo FCD es isósceles, tenemos que FC = CD. Así podemos escribir AF = AC - FC = CE - CD. Por tanto
\frac{CE}{CD}=\frac{CD}{CE-CD}= \frac{1}{CE/CD - 1}
Sustituyendo CE/CD por \phi tenemos
\phi = \frac{1}{\phi-1}\qquad\,(1)
en otras palabras \phi-1=1/\phi. Esta ecuación describe la razón dorada. \phi es el único número positivo que cuando le restamos la unidad, obtenemos su inverso.
De la discusión anterior se desprende: Si en un triángulo isósceles, el ángulo opuesto a la base vale 108°, la razón de la base del triángulo y uno de los otros lados es la razón dorada.

Algunas consideraciones sobre triángulos

Pentagon discussion.svg
Consideremos a un pentágono (regular) y la circunferencia circunscrita a dicho pentágono.


 Tracemos la perpendicular por el centro de la circunferencia al lado DA del pentágono y sea M la

intersección de esta perpendicular con la circunferencia El ángulo AOB mide 360°/5=72° y el ángulo


AOM es su mitad, es decir 36°. El ángulo MOB, suma de estos dos vale 108° y como el triángulo

AOB es isósceles tenemos que
  1. La razón entre el segmento MB y el radio OM de la circunferencia es la razón dorada
  2. \ang BMO = (180^\circ - 108^\circ)/2 = 72^\circ/2 = 36^\circ
Así, sea P la intersección de las rectas OA y MB. El triángulo PMO es isósceles, y la razón entre el


dio OM y el segmento PM es la razón dorada. Finalmente, el triángulo OBP también es isósceles, con

 lo que PB = OB ( =OM). Tenemos
\frac{PM}{OM} = \frac{1}{\phi} = \frac{MB-PB}{OM} = \phi - 1
Lo anterior se puede interpretar como una demostración geométrica de la ecuación (1).

Algunas aplicaciones trigonométricas

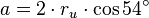
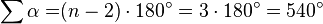
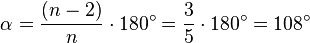
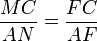
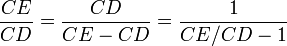
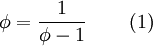
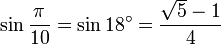
\sin \frac{\pi}{10} = \sin 18^\circ = \frac{\sqrt 5 - 1}{4}
\cos \frac{\pi}{10} = \cos 18^\circ = \frac{\sqrt{2(5 + \sqrt 5)}}{4}
\tan \frac{\pi}{10} = \tan 18^\circ = \frac{\sqrt{5(5 - 2 \sqrt 5)}}{5}
\cot \frac{\pi}{10} = \cot 18^\circ = \sqrt{5 + 2 \sqrt 5}
\sin \frac{\pi}{5} = \sin 36^\circ = \frac{\sqrt{2(5 - \sqrt 5)} }{4}
\cos \frac{\pi}{5} = \cos 36^\circ = \frac{\sqrt 5+1}{4}
\tan \frac{\pi}{5} = \tan 36^\circ = \sqrt{5 - 2\sqrt 5}
\cot \frac{\pi}{5} = \cot 36^\circ = \frac{ \sqrt{5(5 + 2\sqrt 5)}}{5}
Publicado por en

No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)